The Kardashev Scale: An Introduction

A heavily edited (superior) version of this post was published on Astrobites in March 2016. You can read it here.

Theorising about extraterrestrials is hard. Since we only have one data point, our own little civilisation on our own little Earth, trying to pin down what extraterrestrial civilisations will look or behave like stretches the imagination, to put it mildly. But there is one commodity that most theorists agree any advanced civilisation will need in large quantities, and that’s energy. Just over 50 years ago, a Russian astrophysicist named Nikolai Semenovich Kardashev proposed a scale for ranking these hypothetical civilisations based on their energy consumption. The Kardashev scale was intended to help direct searches for signals from intelligent beings, but since its inception has led to hypothetical new energy consumption mechanisms, inspired generations of science fiction writers, and influenced thinking about our own future energy consumption.

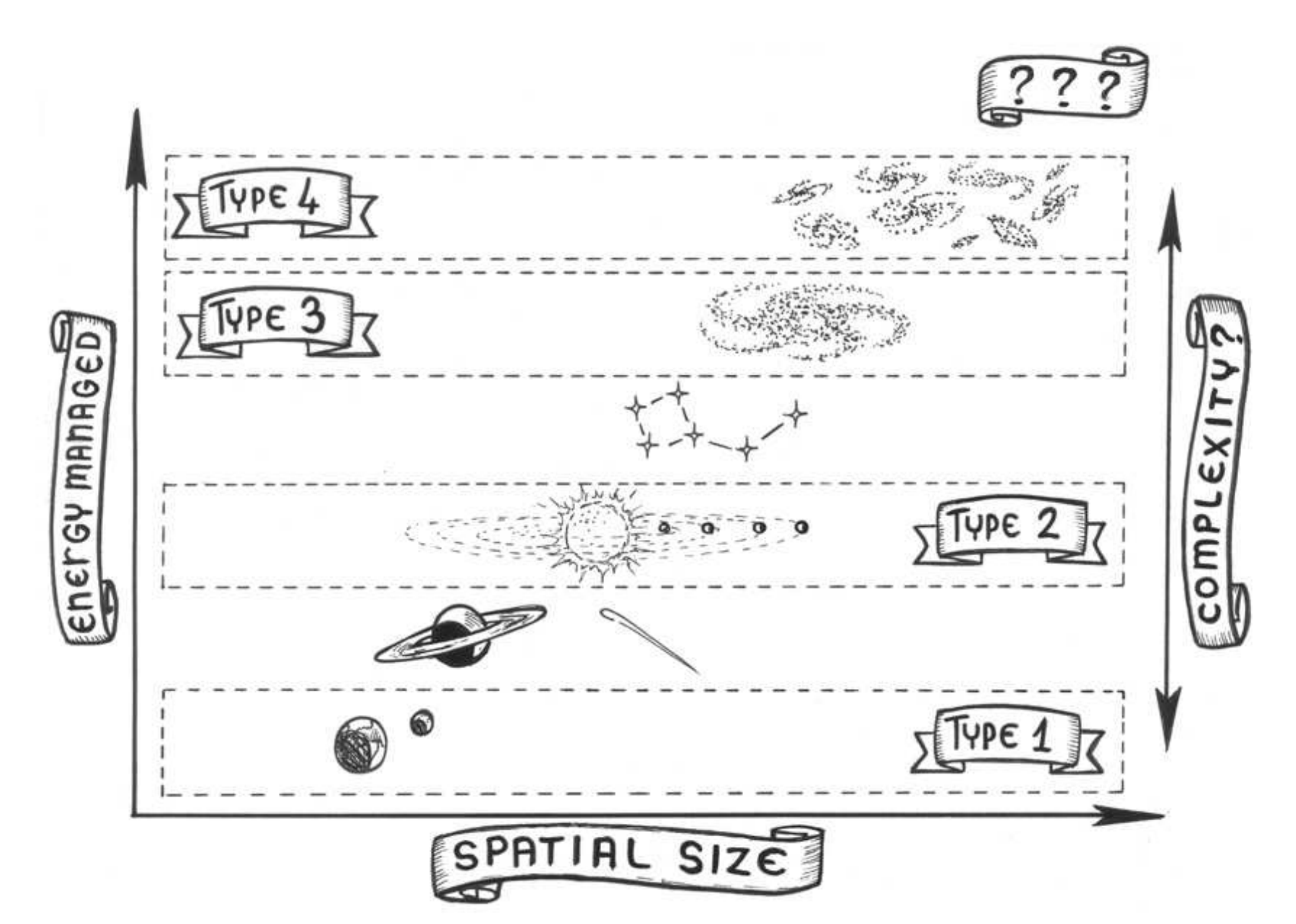
The scale has three types that naturally follow the scale of structures in our local universe. Type I represents a civilisation with complete control over the energy of its host planet; it would, for example, be capable of collecting all the starlight that falls on it. Other than coating a planets surface completely with solar panels, collecting such vast amounts of starlight could be achieved using solar power satellites, transmitting the energy to the surface wirelessly. Power from fusion reactions on an industrial scale could also be used to produce similar amounts of energy over geological timescales.

Type II civilisations have control over the energy of their entire host stars. The engineering challenge of achieving this would be huge, but conceivable structures have been proposed. One of the most famous is the Dyson Sphere, which encompasses an entire star and captures all or the majority of its energy output. Similarly, a Dyson swarm would consist of a vast configuration of solar power satellites surrounding the star.

Type III civilisations blow the first two away, being capable of controlling the energy of an entire galaxy. This could be achieved using a whole population of Dyson spheres around all the stars in a galaxy, or by tapping the energy of the Black Hole at the center of the galaxy. Controlling energy on this scale would require unimaginable feats of engineering, as well as interstellar transportation mechanisms far beyond human capabilities today.

Where does our own civilisation sit on this scale? Kardashev initially proposed that the Earth was close to a Type I, but subsequent reclassifications have taken a more self-critical view. Carl Sagan’s modified Kardashev scale, which allows for continuous values, put the Earth at a meagre 0.7. Some predict that the Earth’s power consumption could hit Type I levels on Sagan’s scale in around 200 years, but we are still incredibly far from realising Type II or III status.

Kardashev’s motivation for coming up with the scale was that if we can understand how advanced civilisations source their energy, we can look for clues that they are harvesting or using it in our observations of stars and galaxies. In fact, his scale provides a crude way of quantifying the detectability of a technological civilisation. Type III civilisations would hypothetically have a huge impact on their host galaxies, and be clearly identifiable due to their interactions with galactic objects such as stars and black holes. More speculatively, the transportation and communication mechanisms such a civilisation might use between these bodies could also be detectable. Recent searches have found no evidence that such a civilisation exists in any galaxies in the local universe.

Dyson spheres would absorb and reemit the energy of the stars that they surround, and this reemitted radiation would have a different spectrum to that seen from the atmospheres of stars. In this case, individual stars could be shown to exhibit artificial features in their emitted light that cannot be explained through the physics of stars we know today, or surveys of collections of stars could be used to identify anomalous spectral features.

Type I civilisations would be the most difficult to detect, due to the lower energies involved, but advances in exoplanet observational techniques could make detections of large artificial energy consumption possible.

Alternatives and extensions to the scale have been proposed, such as Type IV civilisations that can control the energy of the entire universe. Such fanciful propositions have led some to criticise the scale for being speculative; if we cannot understand advanced civilisations, then it is impossible to predict their behaviour. Whilst this is arguably true, what is beyond doubt is the profound impact of such thinking on how we view our own civilisation and the means of powering it. Even if we are alone in the universe, The Kardashev scale has influenced the dialogue surrounding our own civilisations source of energy in the future; if we can avoid destroying our own planet through global warming, or ourselves through nuclear war, how will we power ourselves in to the vast and exciting future?

This post was inspired by a recent paper from Milan M. Cirkovic ‘Kardashev’s Classification at 50+: A Fine Vehicle with Room for Improvement’, which explores the scale, its context and continuing relevance in great detail, as well as this post on Centauri Dreams, which has had me thinking about these topics ever since first reading it.